QuoteCold Fusion was all the rage a few years ago

Raindrop Voltage
But regardless of the scientific principles, the math obviously fails.
The phenomina seems to be more of a word salad generator than any energy source. Somehow rain running across a charged surface to an electrode generates voltage for instance. There are several permutations.
This shows an actual scientific principle is not necessary to generate a scientific paper. You simply methodically observe something and write about it. Observing something does not mean there is anything to see. And since you are observing and scientifically detached, you can be as stupid as hell. Your stupidity becomes a virtue. You can pretend tiny insignificant effects matter since all you are doing is collecting numbers.
The principle invoked in the evaporation process is totally obscure. But they all suffer from the same math problems.
Voltage represents potential energy, but is not a direct measure of energy. Voltage generated by a falling raindrop can't mean shit.
The product of current and voltage together produces power. Both are needed. Voltage without current is meaningless if you are talking about power. Simply charging something up to a high voltage does not mean a lot of energy stored. Even capacitors designed to store electric charge have negligible capacity compared to a battery, any battery.
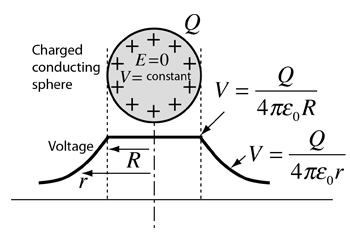
Charge On a Sphere
How much energy does electrostatic energy store?
I think we can agree that a metal sphere a foot in diameter charged to a million volts will have more energy than a raindrop with any electric charge we will find on planet Earth. Orders of magnitude more. A few thousand times more might be a low guess.
The capacitance of an isolated sphere is C = 4πε0r. What does this equation do with a 1 foot metal sphere?
C = 4πϵ0 × 0.1524 meters (0.1524 meters is six inches)
The permittivity of free space, a property of the universe, is 8.85E−12 F / m (Farads per meter) -> that is .00000000000885 Farads per meter.
C = 4π×8.85×10−12 F/m × 0.1524 meters => C ≈ 3.56 × 10−11 F => C = 3.56 × 10−5 microfarads. A microfarad is a millionth of a Farad.
The energy on a capacitor is given by 0.5 × C × V^2. C is capacitance in Farads and V is voltage. In this equation voltage is squared. Using this equation calculates energy.
E = 0.5 × 3.56×10−11 × (1×10E6)^2
E = 1.78 joules (for 1 sphere)
If my computer needs 500 watts to operate, how many 1 foot spheres must I discharge from one million volts in an hour to keep my computer running? There are 3600 joules in a watt-hour. My computer needs 1,800,000 joules.
1,800,000 joules divided by 1.78 joules per sphere, yields 1,011,236 metal spheres. Each a foot in diameter.
Trillions of raindrops would be needed to keep this single computer running. Not billions, trillions when you think about it. Maybe more. We started out with a charge of a million volts, and we still needed a million 1 foot metal spheres to run this computer. Energy goes up with the square of voltage and the raindrop phenomena generates small voltages.
I'll risk saying that there are a few technical problems to work out.
Could a collection area of a square mile in a hurricane run this computer using the obscure phenomena being studied? Maybe. But in a hurricane a windmill a mile in diameter will power a city.
